SINGULARITÉS DES FONCTIONS DIFFÉRENTIABLES (la théorie mathématique et ses applications)

SINGULARITÉS DES FONCTIONS DIFFÉRENTIABLES (la théorie mathématique et ses applications)

De la topologie différentielle à la dynamique qualitative, en passant par la géométrie analytique et la topologie algébrique, les «singularités» ont bien des incarnations en mathématiques; mais cela n’exclut pas une certaine unité: qu’il s’agisse des points où la dérivée d’une application n’est pas de rang maximal, des points où un espace analytique n’est pas lisse, des points où un champ de vecteurs s’annule, on est confronté à une situation dont la géométrie ne se laisse pas découvrir par une simple application du théorème des fonctions implicites (cf. CALCUL INFINITÉSIMAL - Calcul à plusieurs variables, chap. 2 et 3).

Issue des travaux pionniers de Marston Morse, de Hassler Whitney et de René Thom, la théorie des singularités des applications différentiables cherche à répondre aux questions suivantes:

– Peut-on décrire les singularités des éléments d’une famille à l paramètres «suffisamment générale» d’applications indéfiniment différentiables d’une variété N dans une variété P?

– Peut-on décrire de quelle façon ces singularités se transforment les unes dans les autres dans une telle famille lorsque les paramètres varient?

Nous envisagerons surtout le cas des fonctions f à valeurs réelles définies sur une variété compacte N: généralisant une partie de la théorie de Morse, les résultats décrits ci-dessous sont à la base de la théorie des catastrophes élémentaires de René Thom.

Les trois premiers chapitres du présent article répondent à la première question pour l = 0 (pas de paramètres) en montrant que, par une perturbation arbitrairement petite, toute fonction peut être déformée en une fonction dont tous les points singuliers sont non dégénérés (fonctions de Morse).

Le chapitre 4 montre que, par une perturbation arbitrairement petite, toute famille à l paramètres de fonctions (l fini) peut être déformée en une famille de fonctions de «type singulier fini» (T.S.F.): une telle fonction a un nombre fini de points singuliers au voisinage de chacun desquels elle s’écrit comme un polynôme dans des coordonnées locales bien choisies; c’est précisément de ce caractère localement algébrique que vient la possibilité de faire de la géométrie (après complexification, ainsi qu’on l’esquisse au chapitre 9).

Les chapitres 5, 6 et 7 décrivent la théorie du déploiement universel qui permet, après stratification, de répondre à la deuxième question.

Au chapitre 8, on contemple la zoologie des petites codimensions (catastrophes).

Enfin, les chapitres 9 et 10 ébauchent des liens avec d’autres domaines et des généralisations.

Cet article est en connexion étroite avec les articles CALCUL INFINITÉSIMAL - Calcul à plusieurs variables, TOPOLOGIE -Topologie différentielle et VARIÉTÉS DIFFÉRENTIABLES.

1. Points réguliers

Parler de la forme des hypersurfaces de niveau d’une fonction différentiable peut sembler voué à l’échec en fonction du théorème suivant, dû à Hassler Whitney: Étant donné un fermé F de Rⁿ , il existe une fonction f : RⁿR de classe C 秊 telle que f ^-1(0) = F; le caractère C 秊 de f n’est pas, dans cet énoncé, une restriction plus forte que la simple continuité.

La dérivabilité intervient par contre de façon essentielle dans le lemme de Sard qui, étant donné une application f : RⁿR^p, p 諒 n , assure que l’image f ( (f )) de l’ensemble (f ) des points singuliers (on dit aussi critiques) de f (points où la dérivée de f n’est pas de rang p ) est de mesure de Lebesgue nulle dès que f est de classe C^r , avec r 閭 n 漣 p + 1. Si n 麗 p , il est facile de voir que la conclusion vaut pour f (Rⁿ ) dès que f est de classe C¹. Ce lemme est le seul théorème de structure global applicable à toute fonction C 秊 sur Rⁿ (ou sur une variété C 秊); bien que d’énoncé peu géométrique (car, même si f : RR est analytique, l’ensemble f ( (f )) peut être dense dans R), il est très porteur de géométrie: par l’intermédiaire des théorèmes de transversalité de René Thom dans les espaces de jets, il permet de faire de la géométrie sur presque toute fonction C 秊 (dans un sens très fort qui apparaîtra plus loin).

Une première conséquence du lemme de Sard est l’existence, pour toute fonction f : NR de classe C 秊 sur une variété N de classe C 秊, de «beaucoup» de points réguliers, c’est-à-dire de points a 捻 N tels que la dérivée Df (a ) soit une forme linéaire non nulle sur l’espace tangent T^a N de N au point a . Par l’intermédiaire d’une carte locale, on peut supposer, pour l’étude de f au voisinage de a , que N = 行 est un ouvert de Rⁿ ; le point a = (a ¹, ..., aⁿ ) est alors régulier si et seulement si il existe un indice i compris entre 1 et n tel que:

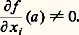Dans ce cas, l’application 切 : 行Rⁿ , définie par:

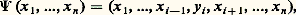où:

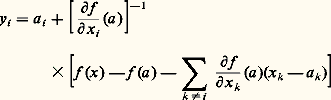vérifie 切(a ) = a , et D 切(a ) est l’identité. D’après le théorème d’inversion locale (qui équivaut au théorème des fonctions implicites), il existe un voisinage 輪 de a dans 行 tel que la restriction 切| size=1^輪 de 切 à 輪 soit un difféomorphisme de 輪 sur 切(face=F0021 輪). Notant 﨏 le difféomorphisme réciproque ( 切| 輪)^-1, on vérifie que, pour tout x 捻 切(face=F0021 輪),

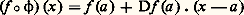autrement dit, le changement de coordonnées local 﨏 transforme f en la partie affine de son développement de Taylor: on dit que le germe de f au point a est déterminé par son jet d’ordre 1. Les définitions précises de ces termes sont données dans la suite de l’article.

Remarquons qu’une conséquence de tout cela est qu’un voisinage de a dans f ^-1(f (a )) est une sous-variété de dimension n 漣 1 de N. On en déduit également un résultat très fort de stabilité : si a est un point régulier d’une application f : NR et si g est assez proche de f au voisinage de a pour la topologie C¹ (c’est-à-dire si g 漣 f et si les 煉(g 漣 f )/ 煉xⁱ , i = 1, ..., n , calculés dans une carte locale au voisinage de a , sont assez petits), il existe b proche de a et un difféomorphisme 﨏 d’un voisinage 輪 de a sur un voisinage 律 de b tel que 﨏(a ) = b , et que g 獵 﨏 soit la restriction de f à 輪.

2. Points singuliers non dégénérés

Sur une variété compacte, une fonction a nécessairement des points singuliers (c’est-à-dire non réguliers), à savoir les extrémums. Nous étudions dans ce chapitre les points singuliers les plus simples (et aussi les plus courants); ainsi que les points réguliers, ils sont caractérisés par une propriété de stabilité et, comme dans bien des cas, la source de cette stabilité est une situation de transversalité : rappelons qu’une application f d’une variété N dans une variété P est transverse en a 捻 N à la sous-variété Q de P, ou bien si f (a ) 殮 Q, ou bien si f (a ) 捻 Q et si l’espace tangent en f (a ) à P est engendré par l’espace tangent en f (a ) à Q et l’image par Df (a ) de l’espace tangent en a à N:

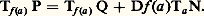Si 﨡 : R^pR^{p -q} est une équation locale de Q au voisinage de f (a ), la condition de transversalité équivaut à dire que D( 﨡 獵 f )(a ) est de rang p 漣 q ; on en déduit immédiatement que, si g est assez proche de f au voisinage de a dans la topologie C¹ et si b est assez proche de a , alors g est encore transverse en b à Q (cf. Transversalité , chapitre 5 de TOPOLOGIE - Topologie différentielle).

À titre d’exemple, étant donné une fonction f : RⁿR de classe C², considérons l’application:

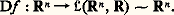La transversalité en a 捻 Rⁿ de Df à la sous-variété réduite au point 0 signifie ou bien que Df (a ) 0, ou bien que Df (a ) = 0 et:

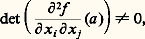qui implique que Df est un difféomorphisme d’un voisinage de a dans Rⁿ sur un voisinage de 0 dans 硫(Rⁿ , R).

Dans ce dernier cas, on dit que a est un point singulier non dégénéré (ou point singulier de Morse ) de f . Remarquons qu’un tel point singulier est isolé et que, si g est assez proche de f au voisinage de a dans la topologie C² (c’est-à-dire pour laquelle toutes les fonctions:

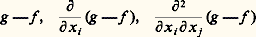sont assez petites au voisinage de a ), il existe un voisinage de a sur lequel l’équation Dg (x ) = 0 a une solution unique b qui est un point singulier non dégénéré de g .

Cependant, contrairement à ce qui se passait pour les points réguliers en vertu du lemme de Sard, une fonction f : RⁿR de classe C 秊 peut très bien avoir tous ses points singuliers dégénérés (c’est-à-dire non «non dégénérés»). Le raisonnement suivant, exemple typique de l’utilisation du lemme de Sard dans les théorèmes de transversalité de Thom, montre qu’on peut remédier à cela par une petite perturbation de f : considérons la sous-variété (c’est un graphe!) V de Rⁿ 憐 硫 (Rⁿ , R) définie par:

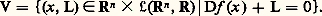D’après le lemme de Sard, il existe L⁰ aussi près que l’on veut de 0 tel que tout point (x , L⁰) appartenant à V soit un point régulier de la restriction à V de la projection de Rⁿ 憐 硫(Rⁿ , R) sur son deuxième facteur; on voit facilement que cela signifie que tous les points singuliers de f + L⁰ sont non dégénérés.

Ce résultat rend plausible le théorème suivant: Soit N une variété compacte de classe C 秊 (il suffit qu’elle soit de classe C²) et soit C 秊(N, R) l’espace des fonctions C 秊 sur N muni de la topologie C 秊 (convergence uniforme de f et de ses dérivées partielles de tous les ordres dans chaque carte d’un atlas de N); l’ensemble des fonctions de Morse (fonctions dont tous les points singuliers sont non dégénérés) est ouvert et dense.

Il est honnête, à ce point, de vérifier que la notion de point singulier non dégénéré garde un sens sur une variété: cette question n’est pas inoffensive car, si la dérivée d’une application f de N dans R a toujours un sens intrinsèque en a 捻 N (car c’est une forme linéaire sur l’espace tangent T^a N), la matrice:

des dérivées secondes de f calculées dans une carte locale n’a de sens intrinsèque que si Df (a ) = 0; il suffit de la calculer après changement de carte pour s’en convaincre. En tout cas, la condition qui définit un point singulier non dégénéré est bien indépendante du choix de la carte locale qui sert à l’exprimer.

3. Espaces de jets et théorèmes de transversalité de Thom

Cette impossibilité de définir intrinsèquement des dérivées d’ordre supérieur autrement qu’à travers une inflation de fibrés tangents de tangents de tangents... a conduit C. Ehresman à introduire, dans les années cinquante, la notion de jet d’application, fondamentale dans le sujet qui nous occupe: la remarque de base est que, si la dérivée k -ième de f en a 捻 N ne peut pas être définie en général comme forme k -linéaire sur T^a N, la propriété pour deux fonctions f et g de coïncider au point a jusqu’à l’ordre k (c’est-à-dire d’avoir en a les mêmes dérivées jusqu’à l’ordre k ) dans une carte locale est indépendante du choix de la carte locale. On dit alors que f et g ont même jet d’ordre k en a ; la classe d’équivalence ainsi définie est appelée jet d’ordre k (ou k -jet) de f au point a , et notée j^kf (a ). L’ensemble des k -jets au point a de fonctions C 秊 sur N est noté Jka (N, R); la réunion disjointe des Jka(N, R), lorsque a parcourt N, est notée J^k (N, R). Si N = Rⁿ , l’application qui à j^kf (a ) associe le couple du point a et du polynôme de Taylor de la fonction X 料 f (a + X) à l’ordre k en 0 (vérifier l’indépendance du choix du représentant f ) identifie canoniquement J^k (Rⁿ , R) au produit de Rⁿ par l’ensemble P^k (n ) des polynômes à n variables de degré inférieur ou égal à k (fig. 1), ce qui munit J^k (Rⁿ , R) d’une topologie. Par exemple J^k (R, R) 力 R^{k +1} , J²(R², R) 力 R⁷, ... On peut en déduire une topologie sur J^k (N, R) qui en fait une variété C 秊, fibrée sur N de fibre J^{k 0}(Rⁿ , R) 力 P^k (n ) (cf. Les espaces fibrés , chapitre 4 de TOPOLOGIE - Topologie algébrique).

L’application J^kf : NJ^k (N, R) qui à x associe j^kf (x ) est alors C 秊. Par le choix d’une carte locale de N, cette application devient:

ce qui nous ramène à l’exemple qui nous a servi de point de départ.

Soit Q la sous-variété de J¹(N, R) formée des jets z de la forme z = j ¹f (x ), Df (x ) = 0 (cette condition ne dépend que de z ). Une fonction f de Morse sur N n’est autre qu’une fonction telle que l’application j ¹f soit en tout point transverse à Q, ce qui explique le caractère intrinsèque de la définition locale du chapitre précédent. Énonçons maintenant, dans le cadre qui nous intéresse, le premier théorème de transversalité de Thom, qui implique immédiatement le théorème de densité des fonctions de Morse énoncé à la fin du chapitre précédent.

Théorème de densité . Si N est une variété compacte, Q une sous-variété fermée de J^k (N, R), l’ensemble des f 捻 C 秊(N, R) tels que j^kf soit en tout point transverse à Q est un ouvert dense.

Il est important de remarquer qu’on ne considère pas dans ce théorème toutes les applications de N dans J^k (N, R), mais seulement celles qui sont «intégrables», c’est-à-dire de la forme j^kg , avec g 捻 C 秊(N, R); la démonstration est une généralisation de celle que nous avons faite à propos des points singuliers de Morse.

4. Points singuliers de détermination finie et fonctions T.S.F.

Nous avons vu dans le premier chapitre que, au voisinage d’un point régulier, une fonction C 秊 est caractérisée, à changement de coordonnées locales près, par son jet d’ordre 1 en ce point; nous étudions maintenant les points singuliers ayant une propriété analogue vis-à-vis du jet à un ordre fini. Nous retrouverons en particulier le lemme de Morse, à la base de si nombreux développements en topologie différentielle.

L’importance de cette question vient de ce que, contrairement à une fonction C 秊 quelconque, une fonction polynomiale est susceptible d’une étude géométrique très précise.

Les résultats étant purement locaux, il est commode d’utiliser le langage des germes : deux applications f et g d’une variété N dans une variété P définissent le même germe en a 捻 N si elles coïncident sur un voisinage de a .

Si P = R^p , l’ensemble C 秊a (N, R^p ) des classes d’équivalence hérite de la structure d’anneau de C 秊(N, R^p ) et est appelé l’anneau des germes en a d’applications C 秊 de N dans R^p . Notons en particulier 劉ⁿ = C 秊⁰ (Rⁿ , R) et désignons par Lⁿ 說 C 秊⁰ (Rⁿ , Rⁿ ) le groupe des germes en 0 d’applications 﨏 : RⁿRⁿ vérifiant 﨏(0) = 0, avec D 﨏(0) inversible; la formule 﨏 練 f = f 獵 﨏^-1 définit une action de Lⁿ sur 劉ⁿ .

L’application f 料 j^kf (0) de Rⁿ dans J^{k 0}(Rⁿ , R) se factorise en une application de 劉ⁿ dans J^{k 0}(Rⁿ , R), encore notée de la même façon (nous confondrons d’ailleurs dans une même notation une fonction et son germe s’il n’y a pas d’ambiguïté sur le point considéré). 劉ⁿ est un anneau local dont l’unique idéal maximal est l’ensemble face=F9828 Mⁿ des germes de fonctions nulles en 0. La formule de Taylor montre que face=F9828 Mⁿ n’est autre que l’idéal engendré par x ¹, ..., xⁿ . Si f 捻 劉ⁿ , on note J(f ) l’idéal de 劉ⁿ engendré par: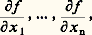

appelé idéal jacobien . Rappelons enfin que, si I et J sont les idéaux engendrés respectivement par 見¹, ..., 見^k et par 廓¹, ..., 廓^l , l’idéal produit IJ est engendré par les 見ⁱ 廓^j , 1 諒 i 諒 k , 1 諒 j 諒 l . Nous pouvons maintenant énoncer le résultat principal de ce chapitre, qui est dû à P. Samuel et à J.-C. Tougeron.

Théorème . Soit f , g 捻 劉ⁿ ; si g 漣 f 捻 face=F9828 Mⁿ J(f )², il existe 﨏 捻 Lⁿ tel que g 獵 﨏 = f . Autrement dit, à changement de coordonnées local près au voisinage de 0, g ne diffère pas de f dès que g 漣 f est «assez petit» dans le sens ci-dessus.

La démonstration est d’un type assez fréquent en théorie des singularités: on considère la «famille à 1 paramètre» de germes f^t = f + t (g 漣 f ), t 捻 [0, 1], joignant f à g , et on cherche 﨏^t 捻 Lⁿ tel que 﨏⁰ = identité, f^t 獵 﨏^t = f pour tout t 捻 [0, 1]; en dérivant par rapport à t et en remarquant que l’hypothèse implique J(f^t ) = J(f ), on obtient 﨏^t en intégrant une équation différentielle ordinaire (ce qui ne nous éloigne pas tellement du théorème des fonctions implicites).

Remarquant que 0 est un point singulier non dégénéré si et seulement si J(f ) = face=F9828 Mⁿ , on déduit de cette proposition le lemme de Morse , c’est-à-dire l’existence d’un changement de coordonnées local au voisinage d’un point singulier non dégénéré (ici 0) transformant f en son polynôme de Taylor en ce point tronqué à l’ordre 2; on exprime encore cela en disant que le germe de f en un point singulier non dégénéré est déterminé par son jet d’ordre 2. On remarque que ce lemme est valable sur une variété et on le comparera à l’énoncé analogue du chapitre 1 dans le cas d’un point régulier. Ce lemme permet une compréhension totale de la géométrie des hypersurfaces de niveau de f au voisinage d’un point singulier non dégénéré; d’autre part, on en déduit le résultat de stabilité annoncé au début du chapitre 2: Si a est un point singulier non dégénéré de f et si g est assez proche de f au voisinage de a dans la topologie C², alors g a un unique point singulier b voisin de a , ce point singulier est non dégénéré (voir chapitre 2) et il existe un voisinage 輪 de a , un voisinage 律 de b et un difféomorphisme 﨏 de 輪 sur 律 tel que:

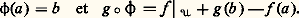Si, plus généralement, étant donné f 捻 劉ⁿ , il existe un entier k vérifiant J(f ) 念 face=F9828 M^kn (ce qui, par le lemme de Nakayama, équivaut à 猪(f ) = dim^R 劉ⁿ /J(f ) 麗 + 秊), alors f est déterminé, à changement de coordonnées local près, par son jet d’ordre 2 k : en effet, face=F9828 MJ²(f ) 念 face=F9828 M^{2k +1}; ce résultat n’est pas le meilleur possible, mais peu importe.

Un tel germe est dit de détermination finie (on dira aussi que 0 est un point singulier de f de détermination finie). En particulier, la topologie des hypersurfaces de niveau de f au voisinage de 0 est la même que pour un polynôme P! Ce polynôme n’est d’ailleurs pas quelconque puisque, si 磊: CⁿC désigne son complexifié, la condition J(f ) 念 face=F9828 M^kn (et donc J(P) 念 face=F9828 M^kn ) équivaut à: 0 est un point singulier topologiquement isolé de P, d’après le Nullstellensatz de Hilbert.

En particulier, un point singulier de détermination finie est isolé; si N est compacte, une fonction f : NR n’ayant que des points singuliers de détermination finie ne peut avoir qu’un nombre fini de points singuliers.

Considérons dans J^{k 0}(Rⁿ , R) l’ensemble ^k formé des jets de la forme z = j^kf (0), avec dim ^R 劉ⁿ /(J(f ) + face=F9828 M^kn ) 閭 k (par exemple, si n = 1, alors J^{k 0}(R, R) s’identifie à l’espace vectoriel de dimension k + 1 des polynômes à une indéterminée, à coefficients réels, de degré 諒 k et ^k est réduit aux polynômes constants); il est facile de voir que cette condition ne dépend que de z et que f 捻 劉ⁿ est de détermination finie si et seulement s’il existe k tel que j^kf (0) 殮 ^k (fig. 1). L’intérêt de cette caractérisation est que ^k est défini par des équations algébriques dans J^{k 0} (Rⁿ , R) 力 R^N: en effet, pour écrire que la codimension du sous-espace vectoriel [J(f ) + face=F9828 M^kn ] / face=F9828 M^{n k +1} de l’espace J^{k 0} (Rⁿ , R) 力 劉ⁿ / face=F9828 M^{n k +1} est supérieure ou égale à k , on annule certains déterminants (mineurs) dont les coefficients sont des dérivées de f en 0, c’est-à-dire de coordonnées de z = j^kf (0) dans J^{k 0} (Rⁿ , R).

Remarquons enfin que, si z = j^kf (0) 捻 ^k et si 﨏 捻 Lⁿ , on a j^k (f 獵 﨏) (0) 捻 ^k ; on en déduit un sous-fibré face=F9828 G^k de J^k (N, R), qui, au-dessus d’une carte locale de N, s’identifie à Rⁿ 憐 ^k 捻 Rⁿ 憐 J^{k 0} (Rⁿ , R) (voir fig. 1 pour le cas n = 1).

Soit 崙 說 C 秊 (N, R) le sous-ensemble formé des fonctions f telles qu’il existe k avec j^kf (N) 惡 face=F9828 G^k = 歷 (fonctions de type singulier fini, ou T.S.F. dans la terminologie de J. Mather). Si N est compacte et si f 捻 崙, alors f n’a qu’un nombre fini de points singuliers, tous de détermination finie, et est donc susceptible d’une étude géométrique.

On peut montrer que, lorsque k tend vers + 秊 la codimension de ^k dans J^{k 0} (Rⁿ , R) tend vers + 秊, on en déduit, à l’aide d’un avatar du théorème de transversalité de Thom, que 崙 est de «codimension infinie» dans le sens où toute famille à un nombre fini de paramètres de fonctions (plus précisément toute application continue d’une variété compacte dans C 秊(N, R)) peut être transformée par une déformation arbitrairement petite en une famille de fonctions T.S.F.

5. Codimension d’une fonction

Nous allons interpréter ce qui précède en termes de l’action sur C 秊(N, R) du groupe G = Diff N 憐 Diff R, produit du groupe des difféomorphismes C 秊 de N par le groupe des difféomorphismes C 秊 de R (changements de coordonnées C 秊 à la source et au but). Ce chapitre 5, sans démonstration, est destiné à rendre plus intuitives les définitions qui seront données au chapitre suivant dans le cadre des germes.

Soit f 捻 C 秊(N, R); nous dirons que f est stable s’il existe un voisinage 輪 de f dans C 秊(N, R) tel que, pour tout g 捻 輪, il existe un difféomorphisme 﨏 de N proche de l’identité et un difféomorphisme 祥 de R proche de l’identité (et même, si l’on veut, égal à l’identité en dehors d’un voisinage du compact f (N)) tels que g = 祥 獵 f 獵 﨏 ^-1. Autrement dit, f est stable si l’orbite locale de f sous l’action du groupe G est ouverte.

Le problème de la stabilité est facile à résoudre dans le cas d’une action 見 : G 憐 MM de classe C 秊 d’un groupe de Lie G sur une variété de dimension finie M: il suit, en effet, du théorème du rang constant (qui découle du théorème des fonctions implicites) que les orbites sont des sous-variétés (images d’immersions injectives). Une condition nécessaire et suffisante de stabilité de m 捻 M est donc la surjectivité de la dérivée en l’élément neutre e de G de l’application A : GM définie par A( 塚) = 見( 塚, m ).

Dans le cas où il n’y a pas stabilité, notons ^m 說 G le stabilisateur de m et choisissons une sous-variété S de M contenant m dont l’espace tangent en m soit un supplémentaire de l’espace tangent en m à l’orbite G 練 m de m . La dimension c (m ) de S, qui n’est autre que la codimension de l’image de DA(e ), est appelée la codimension de m . La restriction à G 憐 S de 見 a une dérivée en (e , m ) de rang maximum (submersion), et elle se factorise au voisinage de (e , m ) à travers un difféomorphisme d’un voisinage de (e , m ) dans (G/ ^m ) 憐 S sur un voisinage 輪 de m dans M.

On en déduit l’existence d’une application C 秊 de 輪 dans S 憐 G, p 料 ((p ), 塚(p )) telle que(p ) = p , 塚(p ) = Id pour tout p dans S 惡 輪, p = 見( 塚(p ), (p )) pour tout p dans 輪. L’étude des orbites au voisinage de m se ramène donc à celle de leur trace sur S. En particulier, toute famille à k paramètres d’éléments de 輪 (c’est-à-dire une application 﨏 : R^k輪 de classe C 秊) s’obtient par action d’une famille à k paramètres d’éléments de G à partir d’une telle famille dans S (fig. 2 pour le cas où k = 1). Le cas où 﨏 est près d’un paramétrage 靖 : R^{c (m )}輪 de S au voisinage de m est particulièrement intéressant: on obtient un résultat de stabilité sur la famille 靖, la famille 﨏 n’en différant pas modulo l’action du groupe après changement de paramétrage (fig. 3).

Dans le problème qui nous occupe, M est remplacé par C 秊(N, R), m par une fonction f et G par Diff N 憐 Diff R. L’espace vectoriel topologique C 秊(N, R) est métrique complet (espace de Fréchet); le rôle de l’espace tangent en l’identité à G est tenu par 臨(N) 憐 臨(R) (en désignant par 臨(V) l’ensemble des champs de vecteurs C 秊 sur V); l’application 見 est ici 見(( 﨏, 祥), f ) = 祥 獵 f 獵 﨏^-1 et la dérivée en e = (Identité, Identité) de A est l’application DA(e ) : 臨(N) 憐 臨(R)C 秊(N, R) définie (fig. 4), après identification du fibré tangent TR à R 憐 R, par:

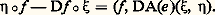Si N = Rⁿ , on peut identifier 﨡 à une application ( 﨡¹, ..., 﨡ⁿ ) de Rⁿ dans Rⁿ , 兀 à une application de R dans R, et on a:

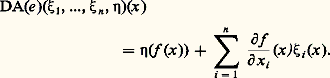On appelle encore codimention de f la codimension dans C 秊(N, R) de l’image de DA(e ).

Malheureusement, le théorème des fonctions implicites, valable dans les espaces de Banach, est en général faux dans les espaces de Fréchet! F. Sergeraert a su cependant adapter le théorème de fonctions implicites raffiné de Nash-Moser à cette situation, et il en a déduit le théorème suivant, formellement analogue à l’énoncé en dimension finie.

Théorème de structure . Soit f 捻 C 秊(N, R) une fonction de codimension finie c ; soit S 說 C 秊(N, R) la sous-variété linéaire formée des fonctions de la forme:

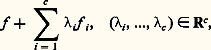où f ¹, ..., f^c engendrent un sous-espace vectoriel de C 秊(N, R) supplémentaire de l’image de DA(e ). Il existe un voisinage 輪 de f dans C 秊(N, R) et une application C 秊 (dans un sens facile à préciser) g 料 (¹(g ), ...,^c (g ), 﨏(g ), 祥(g )) de 輪 dans R^c 憐 Diff N 憐 Diff R telle que toute fonction g dans 輪 s’écrive:

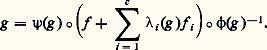L’application définie sur un voisinage de 0 dans R^c par:

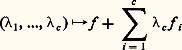(c’est un paramétrage de S) est appelée un déploiement universel de f : toute famille de fonctions contenant f est équivalente, au voisinage de f , à une famille de fonctions de S, modulo l’action d’une famille de changements de coordonnées à la source et au but. Pour étudier géométriquement les petites déformations de f , il suffit donc d’étudier les éléments de S (qui est de dimension finie!).

Il est temps de faire le lien avec les chapitres précédents: les fonctions stables sur une variété compacte sont exactement les fonctions de Morse excellentes , c’est-à-dire les fonctions de Morse dont toutes les valeurs critiques sont distinctes (f ne prend pas la même valeur en deux points singuliers différents). Il est facile de vérifier que ces fonctions forment encore un ouvert dense dans C 秊(N, R). Plus généralement, les fonctions de codimension finie sont exactement les fonctions T.S.F. (qui sont déjà de codimension finie si on remplace Diff N 憐 Diff R par Diff N seul). Le calcul de la codimension de f ne fait intervenir que la restriction de f à un voisinage de l’ensemble (f ) de ses points singuliers (techniquement, on utilise les notions de multigerme et de multijet). Mais il ne suffit pas, bien entendu, d’ajouter les contributions locales de chaque point singulier; il faut encore tenir compte des coïncidences de valeurs critiques: par exemple, une fonction de Morse ayant exactement deux valeurs critiques égales est de codimension 1 (fig. 5).

Le plus gros du problème concerne cependant l’étude du germe de f en un point singulier, et c’est cette étude que nous abordons dans le chapitre suivant. Pour simplifier encore, nous ne considérons que l’action du groupe Diff N: l’image de DA(e ) devient alors l’idéal de C 秊(N, R) engendré dans une carte par les 煉f / 煉xⁱ , i = 1, ..., n , qui n’est autre que l’avatar global de J(f ).

6. Déformation universelle d’un germe de fonction de détermination finie

Le chapitre précédent est censé rendre naturelles les définitions suivantes (Thom, Mather...).

Si f 捻 劉ⁿ , on appelle R-codimension (right-codimension ) de f la codimension dans 劉ⁿ de l’idéal jacobien J(f ) considéré comme sous-espace vectoriel:

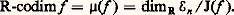Nous supposons cette dimension finie; ce qui équivaut, d’après le chapitre 4, à supposer f de détermination finie. Le R de R-codimension signifie right , c’est-à-dire droite; en effet, on ne considère que l’action «à droite» de Diff Rⁿ définie par 見( 﨏, f ) = f 獵 﨏^-1 en oubliant l’action «à gauche» de Diff R.

On appelle déformation à l paramètres de f un germe F 捻 劉^{n +l} représenté par:

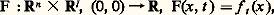dont la restriction f ⁰ à Rⁿ 憐 0 coïncide avec f . Il est important de noter qu’il n’existe pas de topologie sur 劉ⁿ telle qu’une déformation soit une application continue dans 劉ⁿ d’un voisinage de 0 dans R^l : une telle définition serait trop locale, le domaine de définition d’un représentant de f^t , t 捻 R^l , pouvant devenir de plus en plus petit lorsque t s’approche de 0, et laissant échapper les points singuliers que l’on veut étudier (fig. 6); on voit ici pourquoi le problème global se prête mieux à l’intuition géométrique.

Étant donné une déformation F, on lui associe le germe d’application:

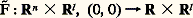défini par 錄(x , t ) = (F(x , t ), t ): on dit que 錄 est le déploiement à l paramètres de f associé à F.

Deux déformations F et G de f sont isomorphes s’il existe un germe de difféomorphisme:

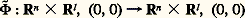de la forme:

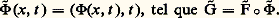On peut interpréter 淋 comme une famille à l paramètres de difféomorphismes définis sur un ouvert fixé de Rⁿ . Remarquons que seul x 料 淋(x , 0) préserve l’origine: demander cela pour tout t revient à considérer l’action sur 劉ⁿ du groupe Lⁿ des germes de difféomorphismes de Rⁿ , 0; l’espace tangent en f à l’orbite de f est ici face=F9828 Mⁿ J(f ). Lorsque 猪(f ) 麗 + 秊, on montre que dim 劉ⁿ / face=F9828 Mⁿ J(f ) 漣 dim 劉ⁿ /J(f ) = n , ce qui correspond aux n degrés de liberté accordés à 淋(x , t ).

Si h : R^m , 0R^l , 0 est un germe d’application, on définit la déformation image réciproque h F de F par la formule h F(x , t ) = F(x , h (t )). Une déformation F de f est dite verselle si toute autre déformation de f est isomorphe à une image réciproque de F; elle est dite universelle (ou miniverselle ) si de plus l = 猪(f ). On voit facilement que, si F et G sont deux déformations universelles de f , F est isomorphe à l’image réciproque de G par un germe de difféomorphisme.

Dans la situation globale du chapitre précédent, un paramétrage régulier de S au voisinage de f mérite le nom de déformation universelle de f .

La notion opposée est celle de déformation triviale , c’est-à-dire telle que f^t soit indépendant de t . La déformation F est triviale si et seulement si 煉F/ 煉t appartient à l’idéal J(F) de 劉^{n +l} , ce qui implique, pour t = 0, que:

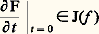et justifie, s’il est besoin, la définition de la codimension de f .

L’analogue du théorème de structure du chapitre 5 s’énonce alors: Soit f 捻 劉ⁿ un germe de R-codimension finie 猪. Une déformation F (à 猪 paramètres) de f est universelle si et seulement si les classes des germes 煉F/ 煉tⁱ (x , 0), i = 1, ..., 猪, engendrent le R-espace vectoriel 劉ⁿ /J(f ).

Nous indiquons une démonstration très simple, due à J. Martinet, de ce théorème dans le cas du germe f 捻 劉¹ défini par f (x ) = xⁿ . Ici J(f ) = face=F9828 M^{1n -1} et 劉¹/J(f ) 力 R^{n -1} est engendré par les classes des germes 1, x , ..., x ^{n -2}; un candidat à être une déformation universelle de f est donc:

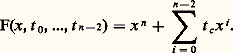Soit G(x , s ) = xⁿ + g(x , s ), avec g (x , 0) = 0, une déformation à 1 paramètre de xⁿ (le cas de l paramètres se traite par récurrence sur l ) et soit:

L’idée est de considérer H comme une déformation de la famille F et de jouer sur la stabilité de cette famille (penser à la figure 3 du chapitre précédent) qui se traduit par la trivialité de toutes ses déformations. Plus précisément, on cherche à construire un germe en 0 de difféomorphisme 切 de R^{n -1} 憐 R de la forme 切(t ⁰, ..., t ^{n -2}, s ) = ( 祥^s (t ⁰, ..., t ^{n -2}), s ), où 祥⁰ est l’identité (famille de difféomorphismes de R^{n -1} au voisinage de 0) tel que H soit isomorphe à l’image réciproque de F par le germe de submersion h : R^{n -1} 憐 RR^{n -1} défini par h (t ⁰, ..., t ^{n -2}, s ) = 祥^{s -1}(t ⁰, ..., t ^{n -2}) (fig. 7).

On en déduira la versalité de F en se restreignant à t = 0.

On note 祥^{s -1}(t ⁰, ..., t ^{n -2}) = (u ⁰(t , s ), ..., u ^{n -2}(t , s )) et on cherche un germe de difféomorphisme 淋 de Rⁿ 憐 R^{n -1} 憐 R de la forme: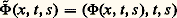

tel que 論 獵 淋 = h F 黎, c’est-à-dire:

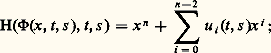ce qui, après composition avec 切, s’écrit:

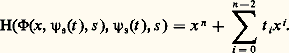En dérivant par rapport à s , il vient une identité de la forme:

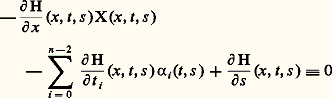(ici, les signes 漣 sont mis pour la commodité des calculs).

Si, réciproquement, on trouve X(x , t , s ), 見^c (t , s ), pour i = 0, ..., n 漣 2, vérifiant cette identité, on construit 切 et 淋 par simple intégration de champs de vecteurs (comparer à l’esquisse de démonstration du lemme de perturbation par face=F9828 MJ² au chapitre 4).

Puisque l’on a:

l’identité ci-dessus s’écrit:

et peut s’interpréter comme une identité de division de 煉H / 煉s par:

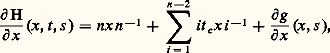qui est une perturbation de nx ^{n -1} par lequel on sait bien diviser.

Si n = 2, cas d’un germe non dégénéré, l’existence de cette division est une simple conséquence du théorème des fonctions implicites: Soit en effet 﨏(t , s ) l’unique germe C 秊 tel que:

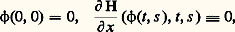qui existe puisque:

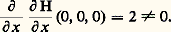On déduit de la formule de Taylor que:

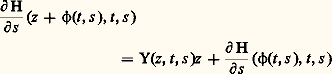et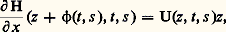

avec U(z , 0, 0) = 2.

Ainsi U(z , t , s )^-1 existe au voisinage de (0, 0, 0) et l’on a:

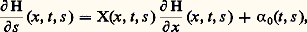avec:

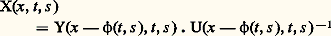et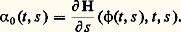

Si n 礪 2, cas d’un germe dégénéré, l’existence de cette division résulte du théorème de B. Malgrange (cf. Étude des idéaux de fonctions différentiables , dans le chapitre 3 de CALCUL INFINITÉSIMAL - Calcul à plusieurs variables): ce théorème généralise au cas différentiable le théorème de préparation de Weierstrass et peut être considéré (comme l’avait prévu R. Thom) comme le théorème de base de la théorie des déformations. Il s’agit de montrer que, si g (x , u ), x 捻 R, est un germe C 秊 vérifiant: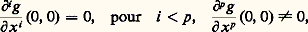

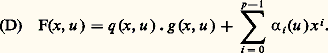et si F(x , u ) est un germe C 秊 quelconque, il existe une identité de division:

De même que ci-dessus (cas n = 2), on s’est ramené à une division par z = x 漣 﨏(u ), on peut ramener (D) à une identité de division par le polynôme générique :

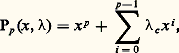où lesⁱ sont considérés comme des paramètres, soit:

On remarque, en effet, que le système d’équations Aⁱ (u ,) = 0, i = 0, ..., p 漣 1, vérifie, lorsque F(x , u ) 令 g (x , u ), la condition: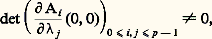

ce qui fournit une solution⁰(u ), ...,^{p -1}(u ) et donc une identité (de Weierstrass) de la forme g (x , u ) = U(x , u ) 練 P^p (x ,(u )), où U inversible, qui permet de passer de (D. P.) à (D). C’est donc dans la division par P^p (x ,) que sont concentrées toutes les difficultés; contrairement au cas holomorphe (Weierstrass), cette division ne peut pas être unique, car le nombre de racines réelles de P^p (x ,) varie avec: pour les valeurs de telles que toutes les racines de P^p (x ,) soient réelles, la division est unique (le reste est donné par le polynôme d’interpolation de Lagrange); le théorème affirme l’existence d’un prolongement de cette division à l’ensemble des valeurs de pour lesquelles certaines racines de P^p (x ,) sont non réelles (on pourra lire la structure de cet ensemble sur les figures 9, 10, 11 pour p = 3, 4, 5).

7. Stratification de C size=5秊(N, R) size=5漣 size=5 et familles «génériques» de fonctions

On peut caractériser les déformations verselles par une propriété de transversalité (comparer à la transversalité de S à l’orbite locale de f au chapitre 5): si f 捻 劉ⁿ est déterminé à difféomorphisme local près par son jet d’ordre k , alors F 捻 劉^{n +l} est une déformation verselle de f si et seulement si l’application 﨏: R^{n +l} 料 J^{k 0}(Rⁿ , R), où 﨏(x , t ) est le jet d’ordre k en 0 de y 料 F(x + y , t ), est transverse en (0, 0) à l’orbite 臨^kf de j^kf (0) sous l’action du groupe L^kn des k -jets en 0 de difféomorphismes locaux de Rⁿ , 0.

Cela pourrait laisser croire que, «en général», une famille de fonctions est un déploiement versel de chacun des éléments de la famille (au niveau des germes ou au niveau global).

S’il en est bien ainsi pour des familles dépendant d’un petit nombre de paramètres, il n’en est rien dans le cas général, car les orbites dans J^{k 0}(Rⁿ , R) (resp. dans C 秊(N, R)) de l’action de L^{k n} (resp. de Diff N 憐 Diff R) forment des familles continues (modules) et, si la transversalité à une sous-variété est une propriété vérifiée «en général», ce n’est plus le cas de la transversalité à toutes les sous-variétés d’une famille (fig. 8).

Il est naturel de chercher à grouper ces familles d’orbites en sous-variétés (ouvertes) formant une partition localement finie (stratification) de J^{k 0}(Rⁿ , R) 漣 ^k (resp. C 秊(N, R) 漣 ) ayant d’assez bonnes propriétés (stratification de Whitney) pour que la transversalité à chacune des sous-variétés de la partition (strate) soit vérifiée «en général». De telles stratifications ont été construites par R. Thom et J. Mather.

Un exemple simple de module nous est fourni par la famille des 4-jets en 0 des fonctions x ³y 漣 xy ³ + tx ²y ² = f^t (x , y ); le birapport des quatre droites f ^{t -1}(0) est un invariant de l’orbite et varie continûment avec t . Remarquons que, dans cet exemple, les germes f^t se déduisent l’un de l’autre par un changement de coordonnées continu (mais non différentiable). Dans le cas général, les éléments d’une même strate auront «même type topologique» (en fait même type topologique universel, ce qui est plus fort) et une famille transverse à la strate sera une déformation topologiquement verselle .

Connaître la géométrie de cette stratification peut alors être considéré comme une réponse à la deuxième question posée dans l’introduction.

Lorsque la codimension est petite, le groupe agit transitivement sur les strates, et la stratification peut être complètement décrite. C’est cette description que nous esquissons dans le chapitre suivant.

8. Classification des germes de petite codimension size=5猪

Appelons stablement équivalents deux germes f 捻 劉ⁿ , g 捻 劉^q tels que f (x ¹, ..., xⁿ ) et g (x ¹, ..., x ^q ) + Q(x ^{q +1}, ..., xⁿ ) soient dans la même orbite de Lⁿ , où Q est un germe de Morse (qu’on peut donc supposer être une forme quadratique non dégénérée). Les théories de déformation de f et g sont analogues car 劉ⁿ /J(f ) 力 劉^q /J(g ). Soit maintenant f 捻 face=F9828 Mⁿ un germe singulier tel que le rang de la matrice:

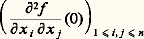soit égal à n 漣 q . À l’aide d’un feuilletage de Rⁿ par des (n 漣 q )-plans transverses au noyau de cette forme quadratique, on peut considérer f comme une déformation à q paramètres d’un germe de Morse dans 劉^{n -q} . L’expression, établie au chapitre 7, de la déformation universelle d’un germe de Morse nous fournit un germe g 捻 face=F9828 M^3q 說 劉^q tel que f et g soient stablement équivalents. On appelle q le corang de f . Cette remarque est fondamentale pour la classification des germes de petite codimension car:

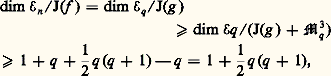puisque J(g ) + face=F9828 M^3q est engendré par les générateurs de face=F9828 M^3q et q polynômes homogènes de degré 2 (le premier terme du développement de Taylor de chacune des dérivées partielles de g ). Par exemple, si 猪 諒 6, on a forcément q 諒 2: c’est le cas pour la théorie des catastrophes élémentaires où 猪 諒 5, ce qui explique que celles-ci soient représentées par des fonctions de 1 ou 2 variables seulement!

En cherchant par quel jet les germes sont déterminés, on arrive facilement à la classification de René Thom (on a supposé f (0) = 0):

猪 = 0 germe régulier,

猪 = 1 germe de Morse,

猪 = 2 germe stablement équivalent à x ³¹ (pli),

猪 = 3 germe stablement équivalent à 梁 x ⁴¹ (fronce ou cusp ),

猪 = 4 germe stablement équivalent à x ⁵¹ (queue d’aronde)

ou à x ³¹ 漣 3x ¹x ²² (ombilic elliptique)

ou à x ³¹ + x ³² (ombilic hyperbolique),

猪 = 5 germe stablement équivalent à 梁 x ⁶¹ (papillon)

ou à x ²¹x ² + x ⁴² (ombilic parabolique).

La déformation universelle de xⁿ a déjà été écrite; des déformations universelles des ombilics sont, par exemple, les suivantes:

ombilic elliptique:

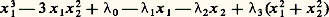ombilic hyperbolique:

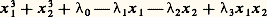ombilic parabolique:

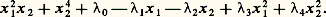Remarquons que tous ces germes sont représentés par des polynômes quasi homogènes; en particulier f 捻 J(f ): une conséquence de cela est l’identité, pour les germes ayant un 猪 petit, entre la théorie des déformations que nous avons considérée (changement de coordonnées à la source seulement) et la théorie dans laquelle on se permet aussi des changements de coordonnées au but; en effet, on déduit de l’expression de DA(e ) donnée au chapitre 5 que, dans cette dernière, J(f ) doit être remplacé par l’espace vectoriel:

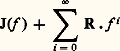qui, dans le cas quasi homogène, se réduit à J(f ) + R 練 1: autrement dit, seul le terme constant de la déformation verselle disparaît, ce qui signifie qu’on ne perd rien en remplaçant l’ensemble des difféomorphismes de R par les seules translations.

Nous pouvons donc utiliser les formules qui précèdent pour décrire la géométrie de la stratification de C 秊(N, R) 漣 par les orbites de Diff N 憐 Diff R au voisinage d’une fonction 肋 dont toutes les valeurs critiques sont distinctes et dont tous les points singuliers sauf un sont de Morse, l’unique point singulier dégénéré ayant une codimension 猪 諒 5. On part d’un des déploiements universels donnés ci-dessus dans lequel on a supprimé le terme constant⁰:

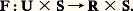Dans ce déploiement universel, U est un voisinage ouvert de 0 dans Rⁿ , n = 1 ou 2, et où S est un voisinage ouvert de 0 dans R 猪 漣1. Soit:

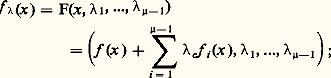ici f désigne le germe de la fonction considérée 肋 au voisinage de son unique point singulier dégénéré, et les classes de 1, f ¹, ..., f size=1^猪 size=1^漣1 engendrent 劉ⁿ /J(f ).

Soit C 說 U 憐 S l’ensemble (algébrique) des couples (x ,) tels que x soit un point singulier de f size=1^凞, c’est-à-dire:

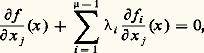pour tout j .

Le début du présent chapitre 8 nous permet de supposer que j ²f (0) = 0 et donc que f^c (x ) = xⁱ pour i = 1, ..., n . On en déduit que C est un graphe, donc une sous-variété C 秊 de U 憐 S. On voit alors facilement que l’ensemble K des points (x ,) 捻 C tels que x soit un point singulier dégénéré de f size=1^凞 n’est autre que l’ensemble des points où la restriction de F à C n’est pas de rang maximal, ou encore l’ensemble des points où la restriction à C de la projection 神 : U 憐 SS n’est pas de rang maximal.

Notons Bif(F), ensemble de bifurcation de F, l’image 神(K) 說 S; c’est l’ensemble des points tels que f size=1^凞 ait au moins un point critique dégénéré. L’image F(C), graphique de F, est une sous-variété algébrique de R 憐 S; la projection sur S de ses points singuliers est la réunion de Bif (F) et de l’ensemble Max(F), ensemble de Maxwell de F, des valeurs de pour lesquelles f size=1^凞 a au moins deux valeurs critiques égales. On peut montrer que, si¹ et² sont dans la même composante connexe de S 漣 [Bif(F) 聆 Max(F)], alors f size=1^凞1 et f size=1^凞2 sont deux fonctions de Morse excellentes se déduisant l’une de l’autre par un changement de coordonnées dans U et une translation de R. Pour obtenir la trace sur S de la stratification cherchée, il suffit donc de décomposer Bif(F) et Max (F) en orbites, ce qui peut se faire explicitement (voir les figures 9 à 13). Il reste à montrer, mais ce n’est pas difficile, que la stratification obtenue au niveau des germes coïncide avec la stratification définie au voisinage de 肋 par les orbites de Diff N 憐 Diff R sur une sous-variété de dimension 猪 漣 1 transverse à l’orbite de 肋 . Pour des fonctions T.S.F. 肋 plus générales, on raisonne de même avec le multigerme de 肋 en ses points singuliers dégénérés.

Les figures 9 et 10 explicitent les constructions ci-dessus pour les germes x ³ et x ⁴.

Les figures suivantes ne concernent que la stratification dans S ou des sections de celle-ci par des plans.

Il apparaît que, comme nous l’avons indiqué dans le chapitre 7, la stratification par les orbites est localement finie pour ces valeurs de 猪.

V. I. Arnold et son école ont montré que la classification des singularités suivant la «modalité» (ou nombre de modules, c’est-à-dire le nombre maximal de paramètres continus dont dépend une famille d’orbites contenant l’orbite considérée) présente une étonnante richesse de structure: par exemple, les singularités sans module (dites singularités simples) sont associées aux groupes de Coxeter Aⁿ , Dⁿ , E⁶, E⁷, E⁸, et donc aux solides platoniciens (Arnold, Critical Points of Smooth Functions ).

9. Lien avec la théorie des déformations des germes d’hypersurfaces analytiques et l’équisingularité

Dans ce chapitre, nous supposons f (0) = 0. Les germes f 捻 劉ⁿ de détermination finie ont été caractérisés par la finitude de 猪(f ) = dim 劉ⁿ /J(f ); on peut montrer que cela équivaut à la finitude de 精(f ) = dim 劉ⁿ /(f , J(f )) où (f , J(f )) désigne l’idéal engendré par les germes de f , 煉f / 煉x ¹, ..., 煉f / 煉xⁿ (cette équivalence est propre au cas où le but est de dimension 1). Si f est analytique complexe, cette dernière condition signifie que 0 est un point singulier de l’hypersurface face="EU Caron" キ ^-1(0) de Cⁿ , où face="EU Caron" キ désigne le complexifié de f .

On peut interpréter 精 comme une codimension (le groupe des germes de difféomorphismes de Rⁿ en 0 est remplacé par le groupe K de Mather): deux germes f et g tels que f (0) = g (0) = 0 sont dans la même orbite si et seulement si f ^-1(0) et g ^-1(0) sont isomorphes au sens de la géométrie algébrique. Il est facile de développer dans ce nouveau cadre une théorie des déformations: l’énoncé classique du théorème de préparation de Weierstrass s’identifie alors (modulo une translation supprimant le terme en x ^{n -1}) au théorème des déformations K-universelles pour le germe xⁿ .

Cette théorie est plus simple que celle du chapitre 8: en particulier, les déploiements K-versels de f 捻 face=F9828 Mⁿ ne sont autres que les déploiements stables comme germes d’application de R^{n +k} dans R^1+k , c’est-à-dire inchangés après perturbation modulo changements de coordonnées C 秊 à la source et au but; cette remarque est d’ailleurs à la base de la classification par J. Mather des germes d’applications stables.

Considérons maintenant un germe holomorphe face="EU Caron" キ : Cⁿ , 0C, 0 de codimension finie et un déploiement K-universel

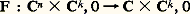de face="EU Caron" キ (la théorie complexe est en tout point analogue à la théorie réelle).

Notons X = 錄^-1(0 憐 C^k ), S = 0 憐 C^k et soit G: X, 0S, 0 la restriction à X de 錄. L’ensemble X est un germe de sous-variété analytique sans singularité de Cⁿ 憐 C^k (c’est un graphe) et on montre que G est un germe d’application stable, qui n’est autre que la déformation universelle de l’hypersurface à singularité isolée face="EU Caron" キ ^-1(0) au sens de la géométrie analytique. La figure 14 faite dans le domaine réel montre la déformation universelle d’un point épais (c’est-à-dire avec multiplicité) qui se déforme en plusieurs points simples.

Finissons cette incursion dans le domaine analytique complexe en effleurant un champ immense, l’étude géométrique des germes d’hypersurfaces analytiques complexes: ce n’est pas s’éloigner du sujet initial puisqu’un germe T.S.F. peut se représenter par un polynôme dans des coordonnées locales bien choisies et donc être complexifié. Le lien entre la géométrie et l’algèbre est incomparablement plus étroit en complexe qu’en réel. Par exemple, si face="EU Caron" キ est le complexifié du germe holomorphe f 捻 劉ⁿ , le nombre 猪(f ) s’interprète comme le degré local en 0 de l’application:

de Cⁿ dans Cⁿ ; on en déduit que, si: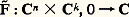

est une déformation (complexe) de face="EU Caron" キ définie sur un petit voisinage U 憐 V de 0 dans Cⁿ 憐 C^k , alors 猪(f ) est le nombre de points singuliers dans U d’une fonction de Morse de la famille (même définition qu’en réel), c’est-à-dire le nombre de points singuliers non dégénérés en lesquels se décompose le point singulier 0 de face="EU Caron" キ .

Une autre interprétation de 猪 est donnée par le théorème de fibration de Milnor: Considérons un germe holomorphe face="EU Caron" キ : Cⁿ , 0C, 0 de codimension finie; si 﨎 est assez petit, la (2 n 漣 1)-sphère S 﨎 de centre 0 et de rayon 﨎 dans Cⁿ = R²ⁿ coupe face="EU Caron" キ ^-1(0) transversalement; l’intersection est donc une sous-variété L de codimension deux de S size=1^﨎. Par exemple, si n = 2, alors L est une réunion disjointe de cercles plongée dans S³; c’est un nœud s’il n’y a qu’un cercle (cas irréductible), un link sinon. L’intersection E size=1^﨎, size=1^兀 de la boule D size=1^﨎 bordée par S size=1^﨎 avec le «cylindre» face="EU Caron" キ ^-1(C size=1^兀), image réciproque du cercle C size=1^兀 de centre 0 et de rayon 兀 très petit, est l’espace total d’une fibration E size=1^﨎, size=1^兀C size=1^兀 définie par z 料 face="EU Caron" キ (z ) (fig. 15). La fibre de cette fibration est une variété de dimension 2 n 漣 2 dont le bord est difféomorphe à L. Un champ de vecteurs dans D size=1^﨎 permet de pousser cette fibre sur S 﨎, et de montrer que l’application:

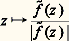restreinte à S size=1^﨎 漣 L est une fibration sur S¹ dont la fibre est difféomorphe à l’intérieur de la fibre précédente.

Toute fibration sur le cercle est obtenue à partir du produit de la fibre 杻 par l’intervalle [0, 1] en identifiant les bords 杻 憐0 et 杻 憐1 par un difféomorphisme de 杻 bien défini à conjugaison près dans le groupe des difféomorphismes. Un tel difféomorphisme est appelé ici «monodromie» de la singularité et a donné lieu à beaucoup de travaux.

Si 0 est un point singulier isolé de face="EU Caron" キ , la fibre de la fibration de Milnor a le type d’homotopie d’un bouquet de 猪( face="EU Caron" キ ) sphères de dimension (n 漣 1). Les (n 漣 1) classes d’homologie correspondantes s’appellent les «cycles évanouissants» de face="EU Caron" キ : des représentants de ces cycles appartenant à E size=1^﨎, size=1^兀 s’évanouissent lorsque 兀 tend vers 0.

Les variétés L obtenues sont très intéressantes: leur structure est bien connue grâce à l’étude de la fibre dont elles sont le bord. Par exemple, lorsque k varie de 1 à 28, les équations:

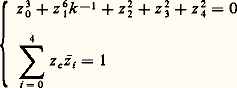définissent des variétés de dimension 7 qui sont homéomorphes à la sphère S⁷ mais ne lui sont pas difféomorphes: ce sont les 28 sphères exotiques de dimension 7 découvertes en 1959 par John Milnor.

Pour montrer encore la richesse de l’invariant 猪( face="EU Caron" キ ), citons le théorème de Lê Dung Tráng et Ramanujam affirmant que, si n 3, une famille de germes d’hypersurfaces de Cⁿ dans laquelle l’invariant 猪 reste constant est équisingulière (le type topologique ne change pas). La restriction n 3 (est-elle réelle?) vient de ce que la démonstration utilise le théorème du h -cobordisme de Stephen Smale.

Dans une telle famille, le type analytique peut varier. D’ailleurs Gabrielov a montré que la dimension en 0 de l’ensemble des valeurs des paramètres d’une déformation universelle de face="EU Caron" キ pour lesquelles face="EU Caron" キ size=1^凞 possède une singularité avec 猪( face="EU Caron" キ size=1^凞) = 猪( face="EU Caron" キ ) est égale à la modalité de face="EU Caron" キ .

10. Le cas des applications

Étant donné deux variétés N et P de classe C 秊, avec N compacte, une application f : NP de classe C 秊 est dite stable si son orbite locale, sous l’action du groupe Diff N 憐 Diff P est ouverte. Lorsque P = R, nous avons vu que les applications stables forment un ouvert dense de C 秊(N, P) et ont pour seules singularités des points de Morse. Dès 1955, H. Whitney a montré que, si N et P sont de dimension deux, les applications stables forment un ouvert dense et ont pour seules singularités des plis et des fronces (fig. 16). Il fallut attendre R. Thom pour avoir les premiers exemples de couples (N, P) pour lesquels les applications stables ne sont pas denses; en fait, seules les dimensions n et p de N et de P interviennent. Utilisant la notion de déploiement K-versel (à laquelle nous avons fait allusion au chapitre 9), J. Mather a pu classer les germes stables en termes algébriques et en déduire pour quels couples (n , p ) les applications stables formaient un sous-ensemble dense de C 秊(N, P) (fig. 17).

Enfin, Thom et Mather ont pu montrer que les applications topologiquement stables (on se permet des changements de coordonnées simplement continus) forment toujours un ouvert dense. L’idée d’une démonstration est que presque toute application f : NP est T.S.F. (c’est-à-dire telle que la restriction de f à son lieu singulier (f ) soit un morphisme fini au sens de la géométrie algébrique, ce qui est la forme globale de la finitude de 精(f ) pour un germe de fonction). Une telle application se plonge dans un déploiement K-versel f : N P qui, grâce à sa stabilité, peut être stratifié. Enfin, pour presque toute f , les sous-variétés N de N et P de P sont transverses aux stratifications de N et de P , ce qui permet de conclure en appliquant un théorème d’isotopie de Thom.

À l’extrême opposé, citons un bel exemple de Thom d’une famille d’applications polynomiales dont le type topologique varie continûment en fonction du paramètre k . On définit f^k : R³R³ par f^k (x , y , z ) = (X, Y, Z), avec:

En géométrie analytique complexe, ces résultats se traduisent par la théorie des déformations des intersections complètes à singularité isolée. Signalons que Grauert a montré en 1972 que tout germe d’espace analytique à singularité isolée a une déformation (plate) universelle; dans le cas général (non-intersection complète), l’exigence de platitude empêche la base S de la déformation d’être lisse.

11. Quelques problèmes globaux

La théorie de Morse a été utilisée avec succès pour résoudre des problèmes de topologie différentielle. Il y a, en effet, un lien étroit entre les points singuliers d’une fonction de Morse f : NR et la topologie de N. Par exemple, la caractéristique d’Euler de N (somme alternée des nombres de Betti) est égale à la somme alternée C⁰ 漣 C¹ + ... + (face=F0019 漣 1)ⁿ Cⁿ , où Cⁱ est le nombre de points singuliers de f d’indice i (l’indice d’un point singulier est l’indice de la forme quadratique des dérivées secondes en ce point, c’est-à-dire le nombre de carrés négatifs dans une diagonalisation).

L’exemple le plus simple est la restriction à la sphère unité de R^{n +1} de l’une des fonctions coordonnées: il y a deux points critiques, un minimum d’indice 0 et un maximum d’indice n ; la caractéristique d’Euler est donc 1 + (face=F0019 漣 1)ⁿ = 0 si n est impair, 2 si n est pair. Réciproquement, une variété compacte possédant une fonction de Morse avec seulement deux points critiques est homéomorphe à une sphère. Utilisant cela, S. Smale a résolu affirmativement en 1965 la conjecture de Poincaré en grande dimension, montrant qu’une variété compacte simplement connexe N de dimension n 閭 5 ayant même homologie que la sphère Sⁿ est homéomorphe à Sⁿ . L’opération fondamentale est l’élimination d’un couple de points singuliers (d’indices consécutifs i et i + 1) d’une fonction de Morse f : NR par une déformation: le modèle de cette opération est la déformation universelle de la singularité pli (voir le chapitre 8). Pour réaliser ce modèle à partir de f , il suffit de plonger dans N un objet géométrique (couple de nappes en bonne position) constitué d’un disque D de dimension i + 1 centré sur le point singulier d d’indice i + 1 et d’un disque A de dimension n 漣 i centré sur le point singulier a d’indice i , dont les bords situés dans une même surface de niveau de f s’intersectent transversalement en un seul point et tels que la restriction de f à D (resp. A) soit une fonction de Morse ayant pour unique point singulier un maximum en d (resp. un minimum en a ). La déformation de f n’a lieu que sur un voisinage de D 聆 A (fig. 18).

Dans le cas non simplement connexe, on se heurte pour plonger ce modèle à des obstructions du type «K-théorie».

Suivant une terminologie de R. Thom, la singularité pli peut être appelée le «centre organisateur» du processus d’élimination (ou de naissance) d’un couple de points singuliers. D’autres problèmes de «retour au centre organisateur» concernant des singularités de plus grande codimension se posent dans la théorie de J. Cerf de la pseudo-isotopie, dont le principal résultat est la connexité, pour n 閭 6, du groupe Diff⁺ Dⁿ des difféomorphismes de classe C 秊, préservant l’orientation, du disque Dⁿ de dimension n .

À propos des singularités d’applications, citons simplement la théorie de Smale-Hirsh de la classification des immersions de variétés ouvertes, considérablement généralisée par Gronov, l’étude initiée par Thom des propriétés homologiques des ensembles singuliers d’une application générique, les recherches d’Eliashberg sur la simplification par chirurgie des lieux singuliers, etc.

Les singularités des applications différentiables ne sont qu’un aspect du monde des singularités; bien d’autres directions de recherche n’ont pas été évoquées, comme la résolution des singularités, les singularités d’équations aux dérivées partielles, celles des champs de vecteurs, celles des feuilletages; enfin, en topologie, la simple opération qui consiste à prendre le cône sur une variété conduit, lorsqu’on cherche à «arrondir les angles», à la riche théorie du cobordisme de Thom et de Pontriaguine.

Notre «centre organisateur» a été le théorème des fonctions implicites ; dictant les résultats à démontrer, fournissant les outils, il est aussi le premier modèle: que sont, après tout, les théories de déformations universelles sinon une vaste généralisation de ce théorème aux situations où seul un espace de dimension finie de déformations empêche de l’appliquer?

Encyclopédie Universelle. 2012.